競技プログラマのための DP 入門
この記事は Competitive Programming Advent Calendar 2014 - PARTAKE の 13 日目の記事です。
はじめに
プログラミングコンテストの問題の題材として DDR (DanceDanceRevolution) が出題されることは少なくありません *1。しかし、活動時間の全てをオンラインジャッジにつぎ込む生活では、DDR を想像することができず、問題の理解に困ってしまうこともあるでしょう。一分一秒を争うこの世界では、致命傷となりかねません。本記事は、そのような状況への対策として執筆されています。*2
問題
あるゲームには図 1 のような 8 つの矢印パネルがついた台があり、図 2 のような譜面が流れてきます。このゲームの遊び方は単純で、矢印が判定エァリアに重なるタァーイミングでパァーノゥを踏む *3 というルールです。
※4 つのパネル(←、↓、↑、→ を 1 セット)を用いるプレースタイルを SP (Single Play) と言い、今回のように 8 つのパネル (上下左右 2 セット) を用いるプレースタイルを DP (Double Play) と言います。この記事はこれがやりたかっただけです、ここまで読んで頂いてありがとうございました。明日の記事は uwitenpen さんで「CodeRunnerの裏側」です。楽しみですね。
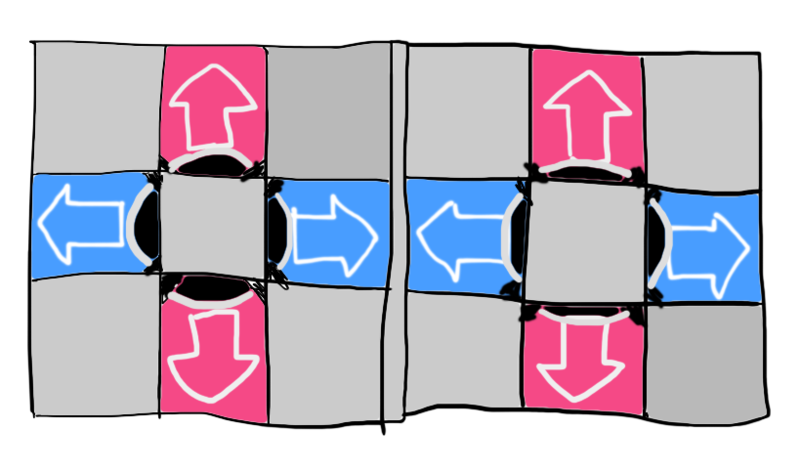
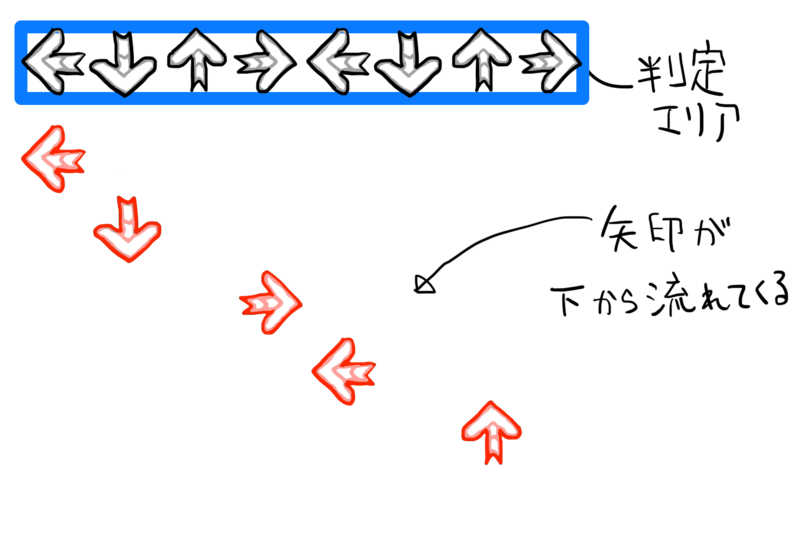
DDR では同時踏みやフリーズアロー(長押し)といった要素もありますが、簡単のためとりあえず考えないことにします。
それぞれの矢印を右足か左足で踏むわけですが、譜面が与えられたときに、どの矢印をどちらの足で踏むことにすれば最も楽に踏めるでしょうか?という問題を考えます。
もちろん「最も楽」の定義がわからない以上、この問題には答えようがないわけですが、以下ではこの「最も楽」の定義を色々と考えてみて、その上でこの問題を解くことを考えます。
「状態」と「遷移」
まずは分かりやすい「最も楽」の指標として次のようなものを考えます。
- 足を動かすときには、距離が長いほど疲れる。
- 足を動かすときには、速さが大きいほど疲れる。
- そこで、足を動かすたびにその距離×速さだけの疲れがたまることにして、最も疲れない踏み方を目指す。
単純な方法として「各矢印について右足で踏むか左足で踏むかをすべて試す」というやり方が考えられますが、これが無駄であることは直感的にもわかると思います。
「100 個目の矢印を踏む足を決めるときに、10 個目とか 20 個目の矢印をどっちの足で踏んだかなんて関係ないのでは?」と感じるのは自然です。この考え方をもう少し進めると
- 100 個目の矢印を踏む足を決めるときに考えないといけないのは、99 個目の矢印を踏んだときに左足と右足がどこのパネルの上にあるかである。
と言えます。ここからが重要なのですが、この考えを逆に
- 99 個目の矢印を踏んだときに左足と右上がどこのパネルの上にあるかさえ分かっていれば、99 個目以前の矢印をどう踏んだかには関係なく 100 個目の矢印を踏む足を決めることができる。
と言ってしまえれば、効率のよい解法への道筋が見えてきます。少し一般的に言うと、「ほげほげさえ分かっていれば、それ以前の詳しいことが分からなくても、その後の選択に何も影響がない」という考え方です。この「ほげほげ」がいわば「状態」を表すのですが、「状態」は今後に影響を及ぼす最小限の要素だけ覚えておけば良いということが大切です。今回の問題の場合「状態」は「ある矢印を踏んだ後に、それぞれの足がどのパネルの上にあるか」です。
dp[k][left][right] を「k 個目の矢印を踏んだ後に、左足が left、右足が right の場所にある」という状態に至るまでの最小の疲れ として、状態間の関係、つまり遷移を考えます。k+1 個目の矢印が pos という場所に流れてくる場合
# 左足を動かして k+1 個目の矢印を踏む場合、その直前に左足があった場所 (left) を全部見て、一番良いものを選ぶ
dp[k+1][pos][right] = min { dp[k][left][right] + 疲れ(left → pos) }
# 右足を動かすときも同様
dp[k+1][left][pos] = min { dp[k][left][right] + 疲れ(right → pos) }
という漸化式が立ちます。あとは k が小さい方からこの式に従って計算を進めていけば問題を解くことができます。この解法のポイントは
- 「それさえ分かっていれば、それ以外の要素はその後の選択に影響を及ぼさない」という最小限の「状態」を見出す
- 「ある状態へ至るまでの最小コスト」を考え、状態間の関係 (ある状態から別の状態へうつる遷移) から漸化式を立てる
でした。
「状態」の拡張
前節で単純な「疲れ」による最適な踏み方の定義をしました。しかし、単に距離や速さによって踏み方の良さを定めるのには限界があります。図 3 のような譜面を考えましょう。
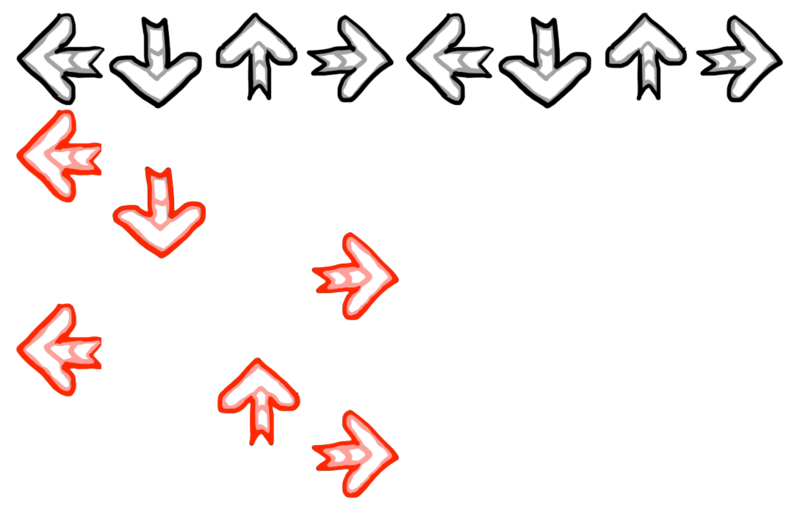
これは「アフロ踏み」と呼ばれる典型的なステップのひとつです。これはどのように踏むのが最適と言えるでしょうか?すこし考えてみましょう。
この配置の踏み方にはいろいろと考えられますが、距離や速さを優先するなら次のような踏み方になるかと思います。
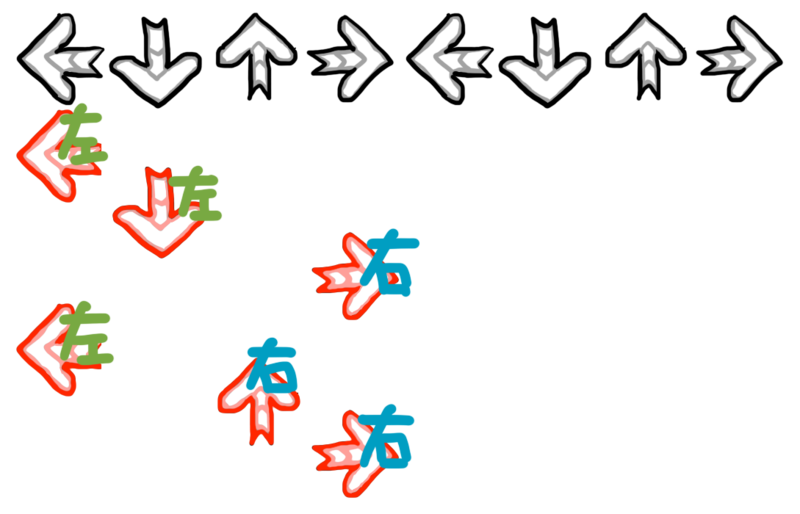
こうすれば左足も右足も、最も近い 2 パネル間の移動だけで済んでいるので、前節の指標であればかなり良いと言えそうです。
しかし、この踏み方では同じ足を連続して使うことが多い点に注意してください。一般に同じ足を連続して動かしてパネルを踏むことをスライドといい、距離や体勢を考えると有用なことも多いですが、同じ足を連続して使うことにより大きな負荷がかかるのはもちろん、動かしていない方の足にも体重が大きくかかり負担となります。そこで、次のような踏み方を考えましょう。
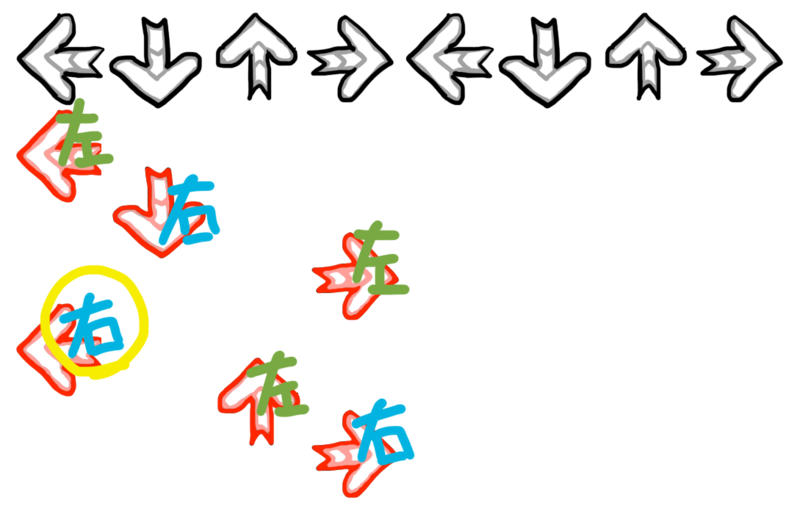
このような踏み方をすると左右の足を交互に使うことができます。
さて、それでは左右に交互に踏むことが最適なのか?というと必ずしもそうではありません。スライドを使った方が足の移動距離が短くなることは多いですし、たとえば先ほどの「アフロ踏み」で交互に踏んだ図 5 を見ると、途中 (丸印を付けた箇所) で身体が横向きになってしまうことがわかります (実際に図 5 に従ってステップを踏んでみましょう)。
「スライド」を多用するのが得意という人もいれば、スライドは苦手なので交互踏みを優先するという人もいるわけです。そういったことも考えた上で、個人の得手不得手も考慮してそれぞれに合った最適な踏み方を導き出すにはどうすればよいでしょうか?
この問題の先ほどと比べて難しいところは、踏み方の良さを考えるにあたって 2 つの評価軸 (スライドの回数と足の移動距離) があるという点に尽きます。このせいで、ある状態へ至るための最良コストを決定することができません。スライドが多くても足の移動距離を節約したい人もいれば、交互に踏めるところはできるだけ交互に踏むという人もいるからです。
今回は状態を拡張することで乗り切ります。これまで状態は「k 個目の矢印を踏んだ後、それぞれの足が置かれている場所」で表現していましたが、これを「k 個目の矢印を踏むまでにスライドを使った回数が s 回で、k 個目の矢印を踏んだ後にそれぞれの足が置かれている場所」とします。つまり、本来評価値であったはずの値 (スライドの回数) を状態に組み込んでしまいます。こうすると、改めて考える評価値は先ほどと同じ移動距離に関するもののみとなり、同じようにして問題を解くことができます。
これができれば、スライドの得意な人にはスライドを多く使った状態へ至るための最適な踏み方を、苦手な人にはスライドをあまり使わない状態へ至るための最適な踏み方を、といった風に個人差を考慮した踏み方を計算することができます。
このように、評価軸が 2 つ以上あるときに、いくつかの評価値を状態に入れてしまうという方法は多くの (動的計画法を用いる) 問題で使うことができます。
奥深き DP の世界
この節は元の問題から少し離れて発展的なトピックです。
図 6 に示す 2 つの譜面パターンを見てみましょう。このように左から右(あるいは逆)に渡り歩くような譜面を「渡り」と言います。
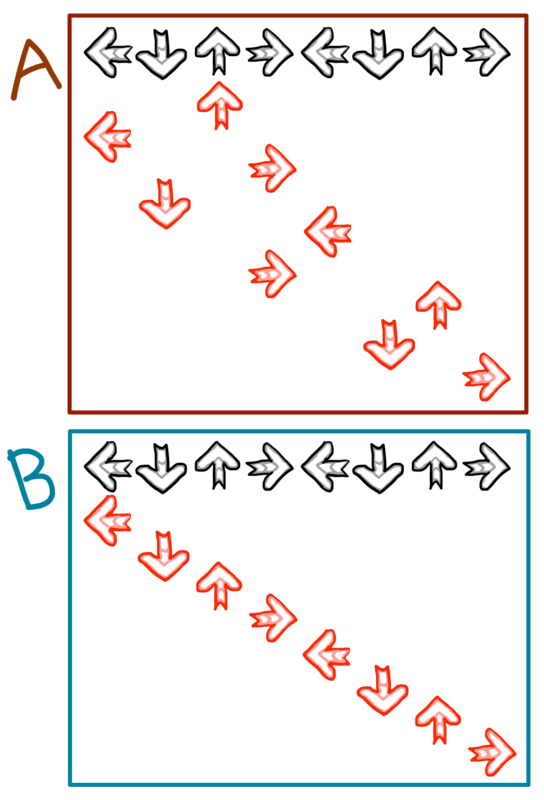
図 7 のようにどちらの足で踏むかを決めてみると、わりと自然と両方とも交互に踏むことができるのが分かると思います。
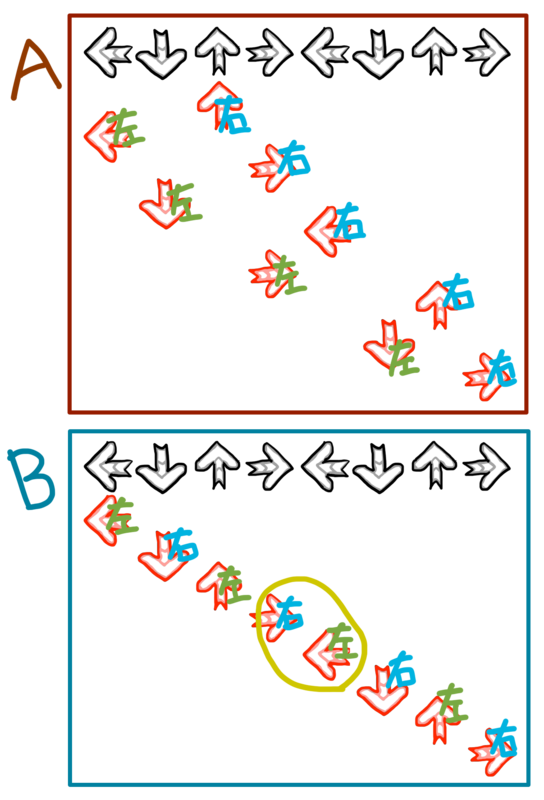
この 2 つのパターンはどちらも交互に踏めている (スライドが 0 回) うえ、足の移動距離も左端近くから右端近くまでとほとんど同じです。ということは、この 2 パターンの譜面の難易度はほぼ同じだと言えるのでしょうか?
実はこの 2 つのパターンでは、A に比べて B の方が難しいとされています。その理由は図 7 の踏み方において囲って示した中央付近のパネルの踏み方にあります。B の譜面では中央あたり (丸印を付けた箇所) で→を右足、←を左足で踏んでいます。実際にステップを踏んでみるとわかりますが、前を向いたままこれを踏もうとすると中央で足が交差します。こういったパターンは交差渡りと呼ばれ、A のようにずっと前を向いたまま自然に踏めるもの (こちらはカニ歩きなどと呼ばれます) に比べて難しいとされているのです。
さらに、交差渡りと一口に言っても、たとえば B の譜面で中央の → を右足で踏んでから左足を交差させて ← を踏みにいくとき、右足の前から交差させていくか後から交差させていくかでも身体の向きが変わります。B のパターンの場合は左足が直前では ↑ パネルにあり、前から交差させていくと身体の向きが渡りの進行方向と合うので、前交差が良い踏み方であると言えます。
こういった配置も考慮に入れて踏み方を考えるときはどのようにすればよいでしょうか?交差するか否かだけであれば、そのときの足の位置から分かりますが、交差するとき前交差か後交差かといった問題は足の位置だけからでは分かりません。状態に新たな要素 (1 歩前だけでなく、2歩前にどの辺に居たか等) を加えるか、あるいは譜面に対して何らかの前処理 (事前に身体の重心の流れを計算しておいて渡りの方向を把握しておく等) をしておくか、などなど、工夫の余地は沢山あると思います。
余談
DDR にはグルーヴレーダーという機能があり、各譜面ごとにその属性 (矢印の密度や、同時踏みの量、長押しの長さなど) が計算されてレーダーチャートで表示されています。このグルーヴレーダーにより難易度や大まかな譜面傾向がつかめる、というわけです。
ところが、8 つのパネルを使う DP では矢印の密度や速さよりも、その配置が何よりも重要になってきます。グルーヴレーダーでは配置に関する情報が何も分からないので、左右に激しく振り回す譜面かどうかといった重要な要素もレーダーからは見て取れません。
そこで、仮に DP の要素に特化したグルーヴレーダーを考えるとしたら、どういった評価軸があって、どういう計算方法がよいかなあと考えていたところ、まさにこの記事に書いたような DP を使って色々な計算ができるのでは?という発想に至り、アドベントカレンダーもそういうネタで書くことに、
決めた、と言いたかったのですが、よく考えると全然 DP 特有の配置の難しさを考えるようなことを記事に書いていないし、なんで書こうと思ったのかよくわからなくなってきました。というかこの記事のほとんどが余談じゃん。皆さん DDR をやりましょう楽しいですよ。