Xmas Contest 2016 C問題 Cutting Swiss Roll 解説
Xmas Contest 2016 C 問題「Cutting Swiss Roll」の解説です。
問題概要
N 要素の整数列 A が与えられ、これを使って 2 人 でゲームをする。ゲームは
- ひとりが A を好きなところで 2 つに切り分け、もうひとりが 2 つに分かれた整数列のうち好きな方を選んで捨てる。
という操作を、切る人と捨てる人を交代しながら交互に行う。最後に長さ 1 の整数列が残ったら終了とする。
先手が最後に残った整数を最大化、後手が最後に残った整数を最小化する戦略をとるとき、最後に残る整数を X とする。
先手の最適戦略 (後手が何をしても最後に X 以上の値を残せる戦略) を実装したプログラムを作成せよ。
制約
- 1 ≦ N ≦ 5,000
- 1 ≦ A[i] ≦ 10^9
解説
最適戦略は X の何になるかを示すときの証明から導くことができるので、X の値を求めよう。
まず、X の値を求めるために二分探索を行うことを考える。つまり、先手が X 以上の値を残せるかどうかの問題を解くことを考える。これは、A の各要素を X 以上なら +1、X 未満なら -1 に置き換えてゲームを行い、先手が +1 を残せるかどうか(残せるならば先手の勝ち)という問題になる。
ここで、この +1, -1 版のゲームの勝敗について以下の定理が成り立つ。この定理の内容は小さいケースを実験するなどして推測できる(何かこの定理に至る良い説明があったら教えてください)。
定理. 以下の 2 条件 (P), (Q) のうちどちらかが成り立つことと、先手が勝つことは同値である:
- (P) A の中にある +1 の個数が -1 の個数より多い。
- (Q) +1 の個数と -1 の個数が等しく、A の先頭 k 個の和 S[k] = A[1] + ... + A[k] が 0 になるような k が偶数個存在する。
この定理では A 全体やその接頭辞における +1, -1 それぞれの個数を問題としているので、定理中で導入した累積和 S を折れ線グラフの形で示したものをゲームの盤面と考えるとわかりやすくなる。
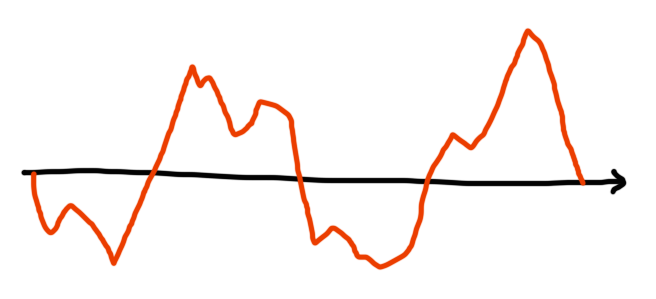
たとえば以下のような状況は条件 (P) が満たされている例である。折れ線の末尾が 0 より大きいところで終わっており、これは A 全体で +1 の個数が -1 の個数より多いことを表している。

また、以下のような状況は条件(Q) が満たされている例である。折れ線の末尾が 0 で終わっており全体としては +1 と -1 の個数が等しく、また先頭を除いた 4 つの箇所で折れ線が 0 と交わっているため、条件 (Q) における k が 4 つ存在している。
上記定理を証明する。証明は整数列の要素数 N についての帰納法による。
N=1 のとき
A = {+1} のとき、何もせず先手の勝ちであり、確かに (P) を満たす。A = {-1} のとき、何もせず先手の負けであり、(P) を満たさない。
N≧2 のとき
A の長さが N-1 以下のときに定理が成り立っていると仮定する。(P) ならば先手必勝、(Q) ならば先手必勝、先手必勝ならば (P) または (Q)、の 3 つを示せばよい。
なおこのゲームでは一回の手番のあと、+1, -1 をすべて反転することで、+1, -1 について対称に考えることができる。つまり、先手必勝であるとは、先手がある場所で切ったあと +1, -1 をすべて反転して、残った左右のどちらも (P), (Q) いずれも満たさない先手必敗の形を押し付けることができる、ということになる。
(P) ⇒ 先手必勝
2 通りの場合がある。まず、S (折れ線) が途中で 0 と交わる場合であるが、このとき先手は最初に S が 0 と交わるところ (青い線) で切ればよい。そうすると、切られた左側・右側のどちらも (+1, -1 を反転して) (P), (Q) いずれも満たさない形になっており、帰納法から両方ともに先手必敗の形である。よって青い線の部分で切れば相手に先手必敗の形を押しつけられるので、全体として先手必勝である。

次に S が途中で 0 と交わらない場合を考える。A の先頭と末尾が両方とも +1 のとき、全体として +1 は -1 より 2 個以上多い。なぜなら、S が途中で 0 になっておらず、最後に正になっているため、S の最後から 2 番目の値も正 (1 以上)であり、よって S の最後の値は 2 以上と言えるからである。したがってこのとき先手は先頭 1 要素だけを切り離すことで、左右どちらも +1 の方が多い形を相手に押しつけられて先手必勝である。
そうでないとき、必ず A の末尾が -1 である。なぜなら、A の先頭が -1 で S の最後の値を正にするためには、途中で S が 0 と交わる必要があるためである。ここで、A 全体を reverse してもゲームとしては全く同じであることに注意すると、A を reverse することで先頭を -1 にできる。reverse しても S の最後の値は正のままなので、reverse することで S を途中で 0 と交わるようにでき、前述のように最初に S が 0 と交わるところで切れば先手必勝である。
(Q) ⇒ 先手必勝
ここでは、S の最後の値が 0 である場合のみについて考える。そのような場合のみに限れば、(Q) と先手必勝が同値であることが示せる。
k=1 のとき、S は以下のような形 (あるいはそれを上下折り返した形) をしているはずである。

このとき、先手がどこで切っても、+1 と -1 の個数を均等に切り分けることはできない (そのように切り分けるには S が 0 のところで切らねばならない)。すなわち、左右のどちらかでは +1 の方が多くなり、もう一方では -1 の方が多くなる。よって相手が -1 の多い方を選択して残すことで勝つことができ、先手は必敗となる。
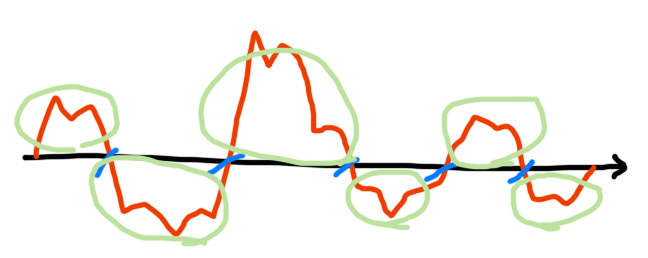
k≧2 のときは S が 0 のところで切る場合のみを考えればよい。なぜなら、そうでない場所で切っても +1, -1 の個数が均等でなくなり負けることが確定するためである。つまり、以下の図で青く示した点のみで切るゲームを考えればよい。

これはつまり、k 個の山 (以下の図で◯で示した部分) を切り分けていき、最後に山 1 個の状態 (k=1) を押しつけられれば勝ちというゲームである。
すると
- k が偶数のとき、k = 奇数 + 奇数 の形に切り分けることで相手に奇数を押しつけられる。
- k が奇数のとき、k = 偶数 + 奇数 と切り分けることしかできず、相手に偶数をとられる。
ことがわかる。k=1 (奇数) を受け取った側が負けることから、(S の最後が 0 という状況下に限れば) k が偶数であること、すなわち条件 (Q) は先手必勝であることと同値である。
先手必勝 ⇒ (P) または (Q)
(P) でも (Q) でもなければ先手必敗であることを示す。
まず (P) ではないので S の最後の値は 0 か負である。負のときは、どこで切っても -1 の多い部分を相手にとられてしまうので必敗である。したがって S の最後の値が 0 であるときを考える。
ところで、先程 S の最後の値が 0 のときに限れば、(Q) は先手必勝と同値であることを示した。ゆえに (Q) ではないことは先手必敗であることを意味する。
したがって (P) でも (Q) でもなければ先手必敗である。
以上で定理が証明された。最後に、具体的な戦略のみをまとめておく。
戦略
まず、上記定理に従って X の値を実際に求め、A[i] を X 以上なら +1、X 以下なら -1 に置き換えておく。すると A は先手必勝 (先手が必ず X 以上を残せる) 形になっているので、あとはこの上で必勝手順を行えばよい。具体的には以下のようにする。
切るとき
まず累積和 S を計算しておく。
- +1 の方が個数が多いなら、S が最初に 0 になる点で切る。そのような点がなければ A を reverse したときの S が最初に 0 になる点で切る。そのような点もなければ最初の 1 要素を切り離す。
- +1 と -1 の個数が同じなら、S が最初に 0 になる点で切る。
選ぶとき
上記定理によって勝敗判定は簡単に行えるので、勝てる方を残す。