GCJ 2015 Round 2 C - Bilingual
グラフと睨めっこしなくてもわりと機械的に作れますという話。
なので、「準備」までは分かっていて最小カットにしたいところまでは前提。
コンテスト中はすぐ作れたので機械的にできると思ってたけど記事を書いてみるとそうでもない気がしてきた。
問題
文章(単語の列)が N 個ある。各文章は英語かフランス語のどちらかである。
英語の文章に出てくる単語はすべて英語の単語で、フランス語の文章に出てくる単語はフランス語の単語である。
文章 1, 2 がそれぞれ英語、フランス語であることが分かっている。
文章 3 … N は分からないが、英語とフランス語で共通する単語の個数を最小にするように文章の言語を決めるとき、その最小値はいくらか。
準備
面倒なので英語、フランス語を E, F と書く。N 個の文章を S_1, S_2, ..., S_N と書く。S_1 = E, S_2 = F で、S_3 … S_N は E, F のどちらか。
入力に出てくる単語 w について、その単語がどの文章に出てきたかを考える。
- 文章 1, 2 の両方に出てくるなら、どうやっても E, F 共通の語(どうでもいいやつ)
- 文章 1 (E) に出てくるが文章 2 (F) に出ないなら、S_3 から S_N のうち w を含むような文章の中に F があれば共通の語(E, F が逆の場合も同じ)
- 文章 1, 2 の両方に出てこないなら、S_3 から S_N のうち w を含むような文章の中に E, F が両方あれば共通の語
やることは、S_3 から S_N までを E のグループと F のグループに分ける。文章の部分集合がいくつかあって、それぞれに対して条件がある。部分集合 A について
1. A が E グループの文章を含めば +1
2. A が F グループの文章を含めば +1
3. A が両グループの文章を含めば +1
のいずれかの形で条件が決まる。
グラフの作り方
※以下では E, F をそれぞれフローの source と sink の意味でも使います。
重要なこと
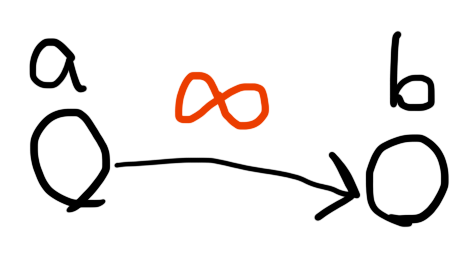
容量無限の辺は
- a が E なら b も E
- b が F なら a も F
を意味する(切ってしまうとカットが無限になる)。
E を含めば +1
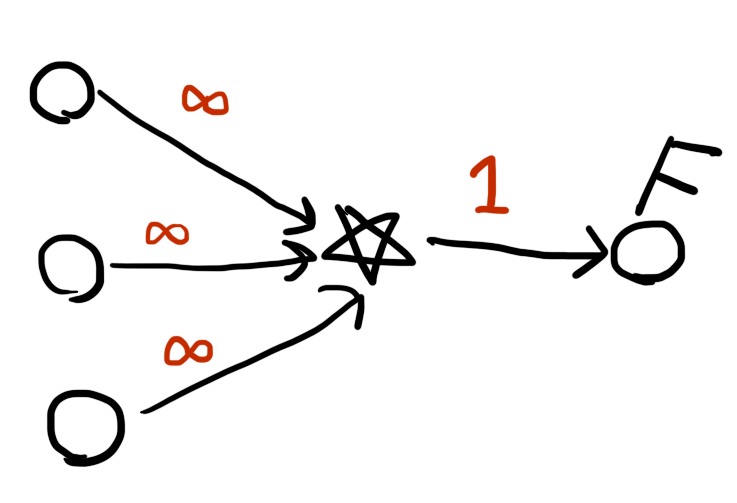
たとえば a, b, c のうち誰かが E なら +1 というコストをつけたいときは
- a, b, c のうち誰かが E なら必ず E になる点(☆)を作って
- ☆から F に容量 1 の辺を張る
☆の作り方は「重要なこと」を使うと簡単。
F を含めば +1 も同じようにできる。
両方含めば +1
文章の部分集合が空でないから E か F のどちらか片方は少なくともあるので
- E を含めば +1
- F を含めば +1
の両方をやって、答から 1 を引く。